Counting Triangles

One of my favorite Project Euler problems is the Counting Triangles problem, both because it requires geometric intuition, and it is deceptively simple.

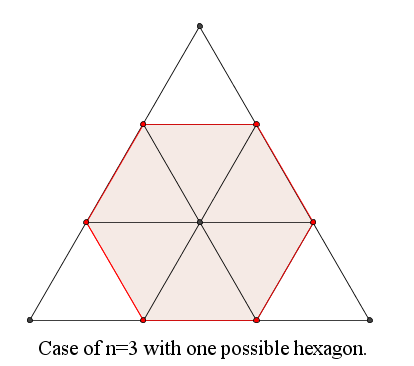
An equilateral triangle with integer side length $n \geq 3$ is divided into $n^2$ equilateral triangles with side length 1 as shown in the diagram below.

The vertices of this triangle constitute a triangular lattice with $\frac{(n+1)(n+2)}{2}$ lattice points.

Let $H(n)$ be the number of all regular hexagons that can be found by connecting 6 of these points.

For example, $H(3) = 1, H(6) = 12$, and $H(20) = 966$.

Find $\sum_{n=3}^{12345} H(n)$.

Note

If you haven’t tried solving this problem, please try yourself.

Solution

Basic problem formulation

First, let’s assume that there are no simplifications we can do to the summation, that is, we compute $H(n)$ for every $n$:

def main():
    print(sum([h(n) for n in range(3, 12346)]))

(We use 12346 as the upper bound rather than 12345, because the upper bound is exclusive in Python’s range).

Multiple hexagon sizes

First, let’s break down the problem into more manageable subgoals. By inspection, one can find that the side length for a hexagon is at most $\lfloor \frac{n}{3} \rfloor$. The minimum hexagon side length is, of course, $1$. Assume we have a function num_hex_tiles(n, i) which gives us the number of triangles of size $i$ that can fit in a triangle of size $n$. Our solution would then be:

def h(n: int) -> int:
    return sum([num_hex_tiles(n, i) for i in range(1, n // 3 + 1)])

Hexagonal translation

A reasonable way to start this problem is to think recursively. What are our base cases? What are our recursive cases?

Let’s begin by considering how many hexagons of side length $1$ can fit inside a triangle of side length $n$ - let’s call this quantity $H_1(n)$. For $n = 1$ and $n = 2$, the number of tiling hexagons is 0:

Say we add an additional row to the triangle on the bottom, making $n = 4$. In addition to the current position of our hexagon, we could either move it down to the left, or down to the right. Hence,

If we add an additional layer, there are three additional spots that our triangle could be in:

At every additional hereafter, we add $n - 2$ more rows. Hence, we can express $H_1$ in a summation:

What about $H_2(n)$? The minimum $n$ is no longer 3 - the minimum $n$ is 6.

Since the minimum triangle length increases by 3 every time the hexagon side length increases by 1, a general formula for $H_l(n)$ can be written as:

Or in code:

def sum_1_to_n(n: int) -> int:
    return n * (n + 1) // 2
    
def num_hex_tiles(n: int, hexagon_size: int) -> int:
    # An enclosing triangle side length must be at least 3 times as long as an enclosed hexagon
    if n < 3*hexagon_size:
        return 0
    else:
        return sum_1_to_n(n - 3*hexagon_size + 1)

Hexagonal rotation

Finally, one complication is that hexagons can be placed diagonally. For example:

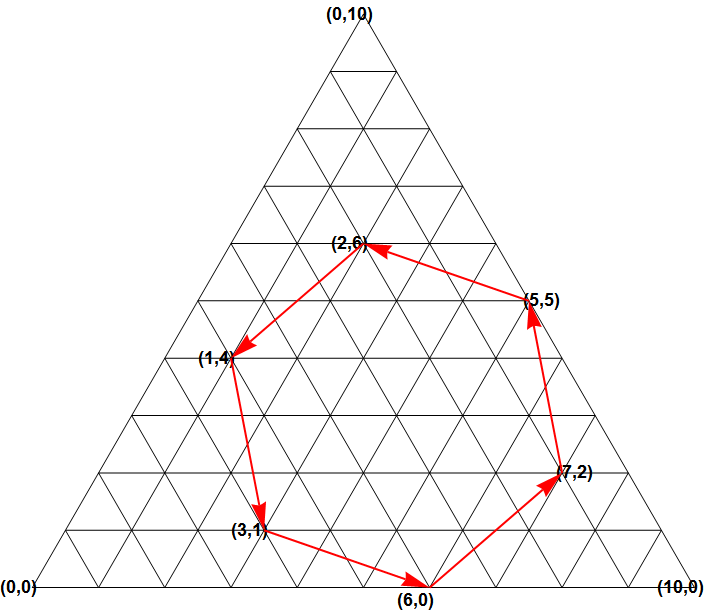
Fortunately, the solution is simple. All the points that constitute a hexagonal rotation lie on the hexagonal edge. That is, you can form a rotation by shifting each vertex along its corresponding edge. For a hexagon of size $n$, there are $n$ rotations possible. We can get our final hexagon-counting function by multiplying each count by the hexagon length.

def num_hex_tiles(n: int, hexagon_size: int) -> int:
    if n < 3*hexagon_size:
        return 0
    else:
        return hexagon_size * sum_1_to_n(n - 3*hexagon_size + 1)

And with this, we are done.

Full code listing

def sum_1_to_n(n: int) -> int:
    return n * (n + 1) // 2

def num_hex_tiles(n: int, hexagon_size: int) -> int:
    if n < 3*hexagon_size:
        return 0
    else:
        return hexagon_size * sum_1_to_n(n - 3*hexagon_size + 1)
        
def h(n: int) -> int:
    return sum([num_hex_tiles(n, i) for i in range(1, n // 3 + 1)])
    
print(sum([h(n) for n in range(3, 12346)]))

This code executes on my laptop in 12.6 seconds. Further optimization is possible, but that’s left to an exercise for the reader :)