Intermediate Dynamic Programming

In my last post, I introduced some basic ideas of dynamic programming and showed how efficient algorithms can emerge from this concept of table-filling. The goal of this blog post is to extend this idea of table-filling to two-dimensional tables, as well as to trees. In this post, I also want to introduce the concept of decorator-based memoization, to simplify DP code.

Longest common subsequence

A subsequence is defined to be a sequence that appears in the same relative order, but is not necessarily contiguous. For example, say our sequence was the string $s = \text{ABCDEFG}$ . Some valid subsequences of $s$ are:

$\text{ABEF}$ ,
$\text{BFG}$ ,
$\text{CDEG}$ .

A common subsequence is a subsequence which is shared between two sequences. For example, say we have two strings $x = \text{ABCDGH}$ and $y = \text{AEDFHR}$ . A few valid subsequences of $x$ and $y$ include:

$\text{AH}$ ,
$\text{A}$ ,
$\text{ADH}$ .

Notably, $\text{ADH}$ is the longest of all of the common subsequences of $x$ and $y$ .

The goal of this problem, is, given two arbitrary strings $x$ and $y$ , find the length of their longest common subsequence (LCS). This is a classic computer science problem, used in diff programs for the version control system Git, and also used in bioinformatics to determine addition/deletion distance between protein sequences.

Brute-force solution

The brute-force solution generates all $2^n$ subsequences of a length- $n$ string, and then checks every pair of subsequences in $O((2^n)^2) = O(2^{2n})$ time. This is clearly intractable.

Recursive formulation

Let’s make a few observations:

The LCS of a string with an empty string is always 0.
If two strings have the same first letter, we can express their LCS length in a simple recursive fashion: $LCS(\text{ABCDE}, \text{AGHFK}) = 1 + LCS(\text{BCDE}, \text{GHFK})$ .
If two strings do not have the same first letter, e.g. , there are two cases:
1. The longest substring is contained in the pair $(x_{2:n}, y)$ : $LCS(\text{BFE}, \text{BFGD})$
2. The longest substring is contained in the pair $(x, y_{2:n})$ : $LCS(\text{ABFE}, \text{FGD})$

This leads us to our recursive formulation:

$LCS(x, y) = \begin{cases} 0 &\text{if $x$ or $y$ are empty}\\ 1 + LCS(x_{2:n}, y_{2:n}) &\text{if }x_1 == y_1 \\ \max (LCS(x_{2:n}, y), LCS(x, y_{2:n})) &\text{otherwise} \end{cases}$

In Python, we can implement these recursive cases in a very straightforward way.

def lcs(x, y):
    if len(x) == 0 or len(y) == 0: return 0
    if x[0] == y[0]:
        return 1 + lcs(x[1:], y[1:])
    else:
        return max(lcs(x[1:], y), lcs(x, y[1:]))

However, as you might have guessed, there are overlapping subproblems in this problem.

As is the usual case, we want a table-filling algorithm which fills the table according to our rules. The key difference between the approach we take here, and the approach shown in the last post, is that here the table is two-dimensional. We use one dimension to represent one string, and the other dimension to represent the other string. Notably, the strings appear in reversed order here, since we are “building up” from smaller strings rather than using a recursive, top-down view.

When the corresponding letters are equal, the algorithm correctly adds one to the digit above and to the left of it. When the letters are not equal, then the max of the top and left digits are taken.

Recursive DP with decorators

Specifying the algorithm in the table-filling fashion (from the bottom-up) can be often prone to errors. Is there a type of table-filling procedure compatible with our recursive Python program?

It turns out, there is. The idea is this:

Create a dictionary, which will serve as our cache.
If the function call arguments are in the cache keys, return that corresponding value.
Otherwise, compute the function call, and store the result in the cache.

In Python, this can be done using decorators. A decorator is a function which returns another, modified function.

@memoize
def lcs(x, y):
    if len(x) == 0 or len(y) == 0: return 0
    if x[0] == y[0]:
        return 1 + lcs(x[1:], y[1:])
    else:
        return max(lcs(x[1:], y), lcs(x, y[1:]))

Notice that the code is entirely the same as before, but with the added @memoize line. In Python, this is equivalent to the expression:

def lcs(x, y):
    if len(x) == 0 or len(y) == 0: return 0
    if x[0] == y[0]:
        return 1 + lcs(x[1:], y[1:])
    else:
        return max(lcs(x[1:], y), lcs(x, y[1:]))
        
lcs = memoize(lcs)

Meaning, memoize is a function that returns another, modified function. We will need to write this function ourselves. Here’s what the code looks like:

def memoize(original_function):
    cache = {}
    
    def wrapper(*args):
        t_args = tuple(args)
        if t_args in cache:
            return cache[t_args]
            
        result = original_function(*args)
        cache[t_args] = result
        
        return result
        
    return wrapper

Although this looks complex, the operation is straightforward:

Define a cache, which is outside the scope of the function. Hence, this dictionary is persistent across calls to wrapper - we don’t want our cache erased every function call!
Define a function wrapper(*args) to be used in place of original_function. By the way, in Python, *args represents the list of arguments. If you call add(3, 5), *args would be [3, 5].
Convert the *args list into a tuple. A tuple is an immutable list. This is an important step, because in Python list objects are not hashable, but tuple objects are.
Check if the function has been called with the same arguments, and if so, return that function.
Otherwise, compute original_function and save the result in cache.

With this method of memoized functions, we can specify a dynamic programming algorithm in a top-down procedure. This can be advantageous for the following reasons:

It can be significantly simpler to implement than grid-based algorithms.
It looks visually much more like our recursive formulation, leading to less bugs.
It can extrapolate DP to non-tabular data structures, like graphs and trees.

Tree-coloring

In the following problem, nodes in a tree can have a given color, which can either be blue or white. In this setup, no parent-child pair can have two blue nodes. The goal of the problem is to maximize the number of blue nodes in the graph.

Some interesting cases:

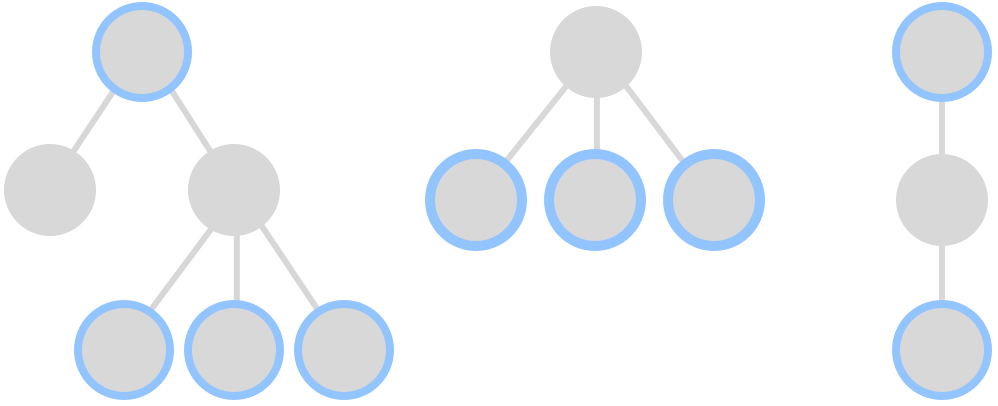
Notably, sometimes the root is colored, and other times it is not colored.

Recursive formulation

Let’s define two variables:

$B_v$ is the optimal solution where the root node $v$ is blue
$W_v$ is the optimal solution where the root node $v$ is not colored blue

Then, the form of our solution is simple: $\max(B_v, W_v)$ .

Now, we have to express a recursive formulation of $B_v$ and $W_v$ , in addition to base cases. Let’s start with the base cases first. Clearly, $B_v = 1$ and $W_v = 0$ if $v$ has no children (i.e., is a leaf), and you can only have one blue node in the case where $v$ is colored.

We also know that if $v$ is colored, its children must not be colored:

$B_v = 1 + \sum_{u \in \text{children}(v)} W_u$

And we also know that if $v$ is not colored, it is possible that its children could either be colored or not colored:

$W_v = \sum_{u \in \text{children}(v)} \max(B_u, W_u)$

Therefore, our corresponding code would be incredibly simple:

@memoize
def B(v):
    if len(v.children) == 0:
        return 1
    else:
        return 1 + sum([W(u) for u in v.children])

@memoize
def W(v):
    if len(v.children) == 0:
        return 0
    else:
        return sum([max(B(u), W(u)) for u in v.children])

Note how easy memoize makes the implementation for us. We do not need to construct a tree of subproblems ourselves - memoize does that for us.

In this post, we discussed doing DP in the case with a grid of values and also with a tree of values. We also introduced decorator-based caching methods, which can be used to express our code recursively while still having table-filling behavior. The final post in this series explores an application of dynamic programming in reinforcement learning.